Day 3: Amidst the stars, Jordan, the space engineer extraordinaire, calculates the volume of a new satellite, a shiny orb with a radius of 1.35 meters. What's the volume of this celestial traveler?
Another really easy formula and calculation for today. We are looking at how to calculate the volume of a sphere. And we're going to take some of the lessons we learned from yesterday and use them to make our RPN data entry super neat and tidy.
Recall the formula for calculating the volume of a sphere:
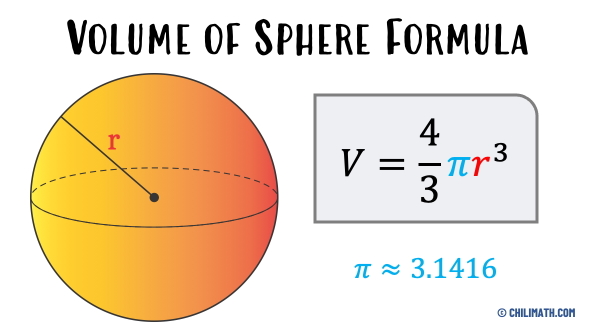
Note the 4/3. This is similar to the 1/3 we saw with the formula of the cone when compared to the volume of a cylinder. Do you see the volume of a cylinder in here? It is there. You have to look closely, because the "*h" is hidden in the r³. Recall in the cone formula this was r², the reason it is cubed now is because we are not multiplying a new value for h, the h value is the radius because we are dealing with a spherical shape (a circle all around), so we fold that into the total r value with another power (another multiplication of the value of r).
So have you noticed something here? This is again the volume of a cylinder with the shape of a sphere being derived from it. I use derived here intentionally because, although I am not going to get into detail with it here, there is a very well developed calculus foundation for why the volume of a sphere is 4/3rds the volume of a cylinder with the same radius. But there is also a geometrically intuitive method, and that is what I wrote about yesterday when we looked at the cone and the cylinder. Today it is the same with the sphere and the cylinder. Although I'd wager that visualizing a sphere as 4/3 of a cylinder is probably much harder than seeing a cone as three parts of a whole cylinder.
Back to our problem.
For common calculators this entire formula can be inputted by the user and the correct answer will be displayed. For those without MathPrint or some version of displaying the functions as they appear in common notation, you would need to use parentheses to ensure a correct calculation. On cheap calculations that do not have a π function, you'd need to manually input 3.14 which would generate rounding errors if precision calculations are required. I do not think there is much of a need to get into this again, you can see the example from yesterday to get an idea how it would be put into the calculator.
Now for RPN. We do not get tied into knots here. Just think about how you look at it and would begin to solve this problem on your own by hand. We've got π, we've got a r (radius) that needs to be cubed, and we have the adjustment for the spherical shape in the form of 4/3. Let's put those on the stack in the same order they come up as we read the equation left to right:

Now there is not a button on the DM32 for directly calculating the cube power of a number. There is a button for squaring but for everything else you have to use the yˣ button and this requires entering 3 (for cubed) on the stack into the x-register.

Note how the function is y^x meaning the value in the y-register will be the base and the value in the x-register will be the exponent. Here is what the result is after we deploy the function:
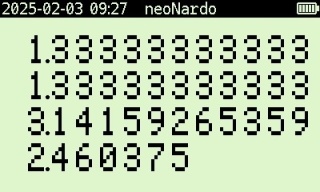
And now we simply execute two multiplication operations because all of our variables are on the stack. Recall that the value in the t-register (the very top) will be pulled-down as the operation is performed on the values within the y-register and x-register (where the multiplication operation performs it's function). So at the very end the value will be displayed in the x-register, and the remaining registers to the top will be filled with this remaining value. This is again a feature of the calculator that is very useful in other calculations we will face down the road.

And so for today's little RPN challenge problem, the volume of Jordan's shiny orb satellite is 10.306m³. Fantastic!
Another really easy formula and calculation for today. We are looking at how to calculate the volume of a sphere. And we're going to take some of the lessons we learned from yesterday and use them to make our RPN data entry super neat and tidy.
Recall the formula for calculating the volume of a sphere:

Note the 4/3. This is similar to the 1/3 we saw with the formula of the cone when compared to the volume of a cylinder. Do you see the volume of a cylinder in here? It is there. You have to look closely, because the "*h" is hidden in the r³. Recall in the cone formula this was r², the reason it is cubed now is because we are not multiplying a new value for h, the h value is the radius because we are dealing with a spherical shape (a circle all around), so we fold that into the total r value with another power (another multiplication of the value of r).
So have you noticed something here? This is again the volume of a cylinder with the shape of a sphere being derived from it. I use derived here intentionally because, although I am not going to get into detail with it here, there is a very well developed calculus foundation for why the volume of a sphere is 4/3rds the volume of a cylinder with the same radius. But there is also a geometrically intuitive method, and that is what I wrote about yesterday when we looked at the cone and the cylinder. Today it is the same with the sphere and the cylinder. Although I'd wager that visualizing a sphere as 4/3 of a cylinder is probably much harder than seeing a cone as three parts of a whole cylinder.
Back to our problem.
For common calculators this entire formula can be inputted by the user and the correct answer will be displayed. For those without MathPrint or some version of displaying the functions as they appear in common notation, you would need to use parentheses to ensure a correct calculation. On cheap calculations that do not have a π function, you'd need to manually input 3.14 which would generate rounding errors if precision calculations are required. I do not think there is much of a need to get into this again, you can see the example from yesterday to get an idea how it would be put into the calculator.
Now for RPN. We do not get tied into knots here. Just think about how you look at it and would begin to solve this problem on your own by hand. We've got π, we've got a r (radius) that needs to be cubed, and we have the adjustment for the spherical shape in the form of 4/3. Let's put those on the stack in the same order they come up as we read the equation left to right:

Now there is not a button on the DM32 for directly calculating the cube power of a number. There is a button for squaring but for everything else you have to use the yˣ button and this requires entering 3 (for cubed) on the stack into the x-register.

Note how the function is y^x meaning the value in the y-register will be the base and the value in the x-register will be the exponent. Here is what the result is after we deploy the function:

And now we simply execute two multiplication operations because all of our variables are on the stack. Recall that the value in the t-register (the very top) will be pulled-down as the operation is performed on the values within the y-register and x-register (where the multiplication operation performs it's function). So at the very end the value will be displayed in the x-register, and the remaining registers to the top will be filled with this remaining value. This is again a feature of the calculator that is very useful in other calculations we will face down the road.

And so for today's little RPN challenge problem, the volume of Jordan's shiny orb satellite is 10.306m³. Fantastic!
Flagged: