Day 2: Dreaming of scoops and success, Mia sketches her vision for "Scoops of Wonder," her future ice cream empire. Her dream cone boasts a radius of 2 cm and a height of 6 cm. How much ice cream can this cone hold?
Recall the formula for calculating the volume of a cone:
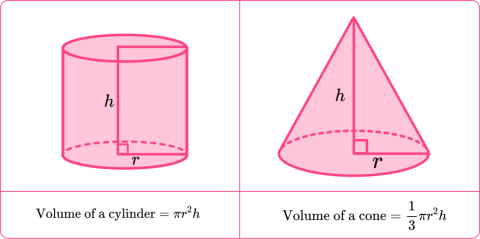
I've included the formula for calculating the volume of a cylinder because there is something important to note about Euclidian geometry (and just might help you remember how to calculate the volume of various shapes). Notice how the formula between the two shapes for volume is exactly the same save for the 1/3 in the cone formula? Imagine if you take the cylinder and sliced it into three separate cones. That is exactly how you are calculating volume with this Euclidian shape, you're calculating the total volume of the cylinder and then cutting out the desired shape's volume from that original calculation. Brilliant.
I like the volume of a cone formula as an example for our second day because many people look at a formula like that with π and a fraction and an exponent (or power) and their eyes begin to slip into the back of their head. But it is actually really easy to use on both a common algebraic calculator and a RPN calculator. Let's take a look.
Most calculators today support some type of fractional input. If not, the user can always calculate 1/3 and continue the calculation of the formula from there. The same holds true for PRN. I can enter fractions into my DM32 with the use of a double-decimal function. The first number entered represents the whole part of the fraction, followed by a decimal input, the second number is the numerator followed by a second decimal input (which tells the calculator it's a fraction input being done and changes the display to represent the whole and fraction part in proper form), with the third number following as the denominator. The benefit of this function is that the calculation will done with the 34-digit mantissa precision which is the true benefit of this particular device.
When I input this formula into my Ti-84 Plus calculator using algebraic MathPrint, the result looks like this:
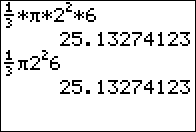
⅓π2²6 which when I hit ENTER yields 25.133 (rounded to three digits). This also works for calculators that do not have implicit multiplication, which would look like this ⅓*C*2²*6. Or calculators that do not feature math print which might look more like this: (0.333)*(3.141)*(2^2)*6. The result will be 25.133 because although the formula looks complicated it is actually a really simple process for the calculator. Volume itself is really not that difficult of a concept, as we saw with the cylinder/cone relationship earlier.
Now using this formula on a common calculator is easy. But I would argue that it is not entirely intuitive. Yes, a student can copy the formula directly from the textbook or computer screen and put it directly into the calculator to yield a result. But nothing is learned in this process, and the tool really only served to give an answer to a particular problem for a student to overcome rather than being initiative for better use and exploration by the user. This makes the device rather useless for professionals or hobbyists beyond school. I think RPN has an edge over this and I'll show you why.
First, let us go back to the cylinder/cone volume relationship. We know that the formula for a cylinder is πr²h. It does not take much to memorize or understand this concept and therefore to recall it when you need it in real life. So let's start with that. For today's problem, we need to calculate the volume of this cone. We know the form will start with the cylinder shape because we know we're deal with a round 3-D shape, so let's plug those number into our calculator.
We have four registers on our screen and so we can put π, r² and h on the stack without any problems. We input π directly from the keyboard and we input 2 and square it using the RIGHT-SHIFT x² key. Next we input the height which is 6. The stack now looks something like this:
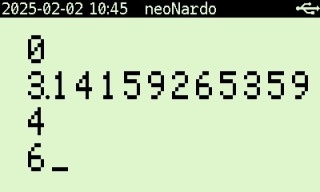
After putting this information on the stack, we use our operation multiplication twice to get the result without the 1/3.

The result is 75.398... which is the volume of a cylinder with the same radius and height as the cone. Now this is where the intuitive part kicks into a higher gear. We can picture in our heads or remember or just think it through again that this cone is really 1/3 of a cylinder that we just calculated with this formula. So we can easily extract the value. With the DM32 I can use the fraction feature to input the value and multiply it by the result we obtained in the steps above. It looks something like this before we multiply:

The final result is 25.133. Which is the same as we got with the common calculator which I guess is important, means they both work.

The truly best part about all of this? Once you get really good at RPN you can load up the stack. This problem really has four parts to it with the 1/3, π, radius squared and height. We have a four-register stack which means all four of these variables can actually be placed on the stack and calculated really easy all at once. The one quark is that because you are loading a variable all of the way to the top (in the aptly named t-register), it will pull down that value as you compute values in the x and y registers (what the multiplication operation takes action on). The loaded stack looks like this:
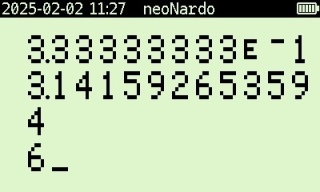
And the following three executions of the multiplication operation we get the result. The y,z and t-registers all have the original value of 1/3 because of that pull-down (which is a feature useful in many other RPN applications). It looks like this:
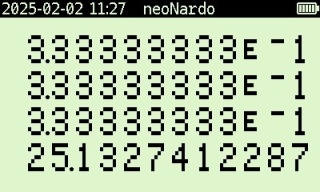
I really do think that the RPN is more efficient and more intuitive. While this a simple problem, you can see that working through the problem is part of how the RPN process works. It is not merely meant to be a copy-paste device to solve problems (that would require you to memorize and recall all sorts of formulas and ways of doing things), rather it works with the user as they work and think through problems they face naturally. This is far more useful for the professional and truly curious.
As we explore more questions and more complicated solutions I think this will become more clear and apparent. For now, we know that Mia's dream cone is just a wee-little over 25cm³.
And Happy Cross Quarter Day (go ahead, look it up)!
Recall the formula for calculating the volume of a cone:

I've included the formula for calculating the volume of a cylinder because there is something important to note about Euclidian geometry (and just might help you remember how to calculate the volume of various shapes). Notice how the formula between the two shapes for volume is exactly the same save for the 1/3 in the cone formula? Imagine if you take the cylinder and sliced it into three separate cones. That is exactly how you are calculating volume with this Euclidian shape, you're calculating the total volume of the cylinder and then cutting out the desired shape's volume from that original calculation. Brilliant.
I like the volume of a cone formula as an example for our second day because many people look at a formula like that with π and a fraction and an exponent (or power) and their eyes begin to slip into the back of their head. But it is actually really easy to use on both a common algebraic calculator and a RPN calculator. Let's take a look.
Most calculators today support some type of fractional input. If not, the user can always calculate 1/3 and continue the calculation of the formula from there. The same holds true for PRN. I can enter fractions into my DM32 with the use of a double-decimal function. The first number entered represents the whole part of the fraction, followed by a decimal input, the second number is the numerator followed by a second decimal input (which tells the calculator it's a fraction input being done and changes the display to represent the whole and fraction part in proper form), with the third number following as the denominator. The benefit of this function is that the calculation will done with the 34-digit mantissa precision which is the true benefit of this particular device.
When I input this formula into my Ti-84 Plus calculator using algebraic MathPrint, the result looks like this:

⅓π2²6 which when I hit ENTER yields 25.133 (rounded to three digits). This also works for calculators that do not have implicit multiplication, which would look like this ⅓*C*2²*6. Or calculators that do not feature math print which might look more like this: (0.333)*(3.141)*(2^2)*6. The result will be 25.133 because although the formula looks complicated it is actually a really simple process for the calculator. Volume itself is really not that difficult of a concept, as we saw with the cylinder/cone relationship earlier.
Now using this formula on a common calculator is easy. But I would argue that it is not entirely intuitive. Yes, a student can copy the formula directly from the textbook or computer screen and put it directly into the calculator to yield a result. But nothing is learned in this process, and the tool really only served to give an answer to a particular problem for a student to overcome rather than being initiative for better use and exploration by the user. This makes the device rather useless for professionals or hobbyists beyond school. I think RPN has an edge over this and I'll show you why.
First, let us go back to the cylinder/cone volume relationship. We know that the formula for a cylinder is πr²h. It does not take much to memorize or understand this concept and therefore to recall it when you need it in real life. So let's start with that. For today's problem, we need to calculate the volume of this cone. We know the form will start with the cylinder shape because we know we're deal with a round 3-D shape, so let's plug those number into our calculator.
We have four registers on our screen and so we can put π, r² and h on the stack without any problems. We input π directly from the keyboard and we input 2 and square it using the RIGHT-SHIFT x² key. Next we input the height which is 6. The stack now looks something like this:

After putting this information on the stack, we use our operation multiplication twice to get the result without the 1/3.

The result is 75.398... which is the volume of a cylinder with the same radius and height as the cone. Now this is where the intuitive part kicks into a higher gear. We can picture in our heads or remember or just think it through again that this cone is really 1/3 of a cylinder that we just calculated with this formula. So we can easily extract the value. With the DM32 I can use the fraction feature to input the value and multiply it by the result we obtained in the steps above. It looks something like this before we multiply:

The final result is 25.133. Which is the same as we got with the common calculator which I guess is important, means they both work.

The truly best part about all of this? Once you get really good at RPN you can load up the stack. This problem really has four parts to it with the 1/3, π, radius squared and height. We have a four-register stack which means all four of these variables can actually be placed on the stack and calculated really easy all at once. The one quark is that because you are loading a variable all of the way to the top (in the aptly named t-register), it will pull down that value as you compute values in the x and y registers (what the multiplication operation takes action on). The loaded stack looks like this:

And the following three executions of the multiplication operation we get the result. The y,z and t-registers all have the original value of 1/3 because of that pull-down (which is a feature useful in many other RPN applications). It looks like this:

I really do think that the RPN is more efficient and more intuitive. While this a simple problem, you can see that working through the problem is part of how the RPN process works. It is not merely meant to be a copy-paste device to solve problems (that would require you to memorize and recall all sorts of formulas and ways of doing things), rather it works with the user as they work and think through problems they face naturally. This is far more useful for the professional and truly curious.
As we explore more questions and more complicated solutions I think this will become more clear and apparent. For now, we know that Mia's dream cone is just a wee-little over 25cm³.
And Happy Cross Quarter Day (go ahead, look it up)!
Flagged: