I am a little busy this morning but managed to find some time to sit down with a cup of coffee and write up a little post. I want to have some fun with the Golden ratio, denoted in mathematics by the Greek letter Phi, on my Ti calculator.
I am not going to get into too much detail about what the Golden ratio is and why it is important. You can read about it in the wiki and I am sure we'll get into it more in the future on the journal. What is important to know is that the ratio is based on the relationship between its parts. It is "golden" because a+b is to a as a is to b. Here is a good image to illustrate it from Wikipedia:
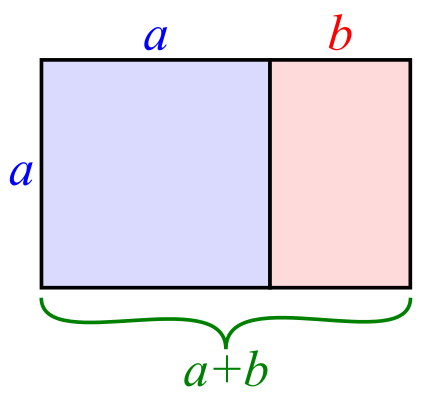
The ratio itself when brought down to the basic elements is a constant in math. It is an irrational number meaning that it goes on forever and has no ending when expressed in digits. It can be calculated by adding 1 to the square root of 5 and dividing the result by 2. It looks like this using pretty Mathprint on the Ti-84 Plus CE (I've stored the result to the alpha-variable P).

This should be pretty straight forward. The result is 1.618... (recall that it is irrational, so it will not have an end, and how many digits you see on your calculator depends on how precise it is). This figure is a ratio so when applying it to a shape like a rectangle you can think of it as 1:1.618... where one side is one unit and the other is a relationship to that single unit. We can get into ratios in the future. Just understand that this number can be applied in many different situations and circumstances using many different units because it represents a relationship between things.
Now let's start to have some fun. And this could make a cool little math trick with your friends. What number can you square and subtract by itself to equal one? You won't find any rational number that will do this. That is because the answer is the Golden ratio. This is because of the relationship of the ratio to the parts. Recall that P=1.618...

We can take this a step further and cube the Golden ratio and then subtract it from the square and itself. The answer is 0. And this is fascinated to me. Again, it is because of the ratio representing the ratio between the parts. The fact that a+b is to a as a is to b.

And we can do this with any series of three powers and the Golden ratio, the answer will always come out to zero.

And if you the super skeptical type and you are still not sure about all of this craziness, you can check it out on the Ti-84 Plus CE equation solver. Simply ask it to give you the variable for an expression where X is cubed, squared and subtracted by itself to equal zero. Keep the results as positive rational numbers (there is an inverse for the Golden ratio but we don't need to get into that now) and you'll get the Golden ratio as the result.

So that was some fun with Phi and I can now see the bottom of my coffee mug. That wasn't too much math, in fact that was hardly none at all. But it is a neat little trick to show a friend and something to play around with on your own calculator if you feel the need. Also, pretty Mathprint.
I am not going to get into too much detail about what the Golden ratio is and why it is important. You can read about it in the wiki and I am sure we'll get into it more in the future on the journal. What is important to know is that the ratio is based on the relationship between its parts. It is "golden" because a+b is to a as a is to b. Here is a good image to illustrate it from Wikipedia:

The ratio itself when brought down to the basic elements is a constant in math. It is an irrational number meaning that it goes on forever and has no ending when expressed in digits. It can be calculated by adding 1 to the square root of 5 and dividing the result by 2. It looks like this using pretty Mathprint on the Ti-84 Plus CE (I've stored the result to the alpha-variable P).

This should be pretty straight forward. The result is 1.618... (recall that it is irrational, so it will not have an end, and how many digits you see on your calculator depends on how precise it is). This figure is a ratio so when applying it to a shape like a rectangle you can think of it as 1:1.618... where one side is one unit and the other is a relationship to that single unit. We can get into ratios in the future. Just understand that this number can be applied in many different situations and circumstances using many different units because it represents a relationship between things.
Now let's start to have some fun. And this could make a cool little math trick with your friends. What number can you square and subtract by itself to equal one? You won't find any rational number that will do this. That is because the answer is the Golden ratio. This is because of the relationship of the ratio to the parts. Recall that P=1.618...

We can take this a step further and cube the Golden ratio and then subtract it from the square and itself. The answer is 0. And this is fascinated to me. Again, it is because of the ratio representing the ratio between the parts. The fact that a+b is to a as a is to b.

And we can do this with any series of three powers and the Golden ratio, the answer will always come out to zero.

And if you the super skeptical type and you are still not sure about all of this craziness, you can check it out on the Ti-84 Plus CE equation solver. Simply ask it to give you the variable for an expression where X is cubed, squared and subtracted by itself to equal zero. Keep the results as positive rational numbers (there is an inverse for the Golden ratio but we don't need to get into that now) and you'll get the Golden ratio as the result.

So that was some fun with Phi and I can now see the bottom of my coffee mug. That wasn't too much math, in fact that was hardly none at all. But it is a neat little trick to show a friend and something to play around with on your own calculator if you feel the need. Also, pretty Mathprint.